image.png

• 左上角的点（TPR=1，FPR=0），为完美分类，也就是这个医生医术高明，诊断全对；
• 点A（TPR>FPR），医生A的判断大体是正确的；
• 中线上的点代表医生给的结果与随机按照一定比例报告病人患病的结果是一样的，从左下角到右上角分别代表随机的比例是0%到100%，随机比例是50%时才代表一半对一半错，即图像中正中间的那个点。当图中点B位于0.5的位置时（TPR=FPR），也就是医生B全都是蒙的，蒙对一半，蒙错一半；
• 下半平面的点C（TPR<FPR），这个医生说你有病，那么你很可能没有病，医生C的话我们要反着听，为真庸医。

上图中一个阈值，得到一个点。现在我们需要一个独立于阈值的评价指标来衡量这个医生的医术如何，也就是遍历所有的阈值，得到ROC曲线。还是一开始的那幅图，假设如下就是某个医生的诊断统计图，直线代表阈值。我们遍历所有的阈值，能够在ROC平面上得到如下的ROC曲线。

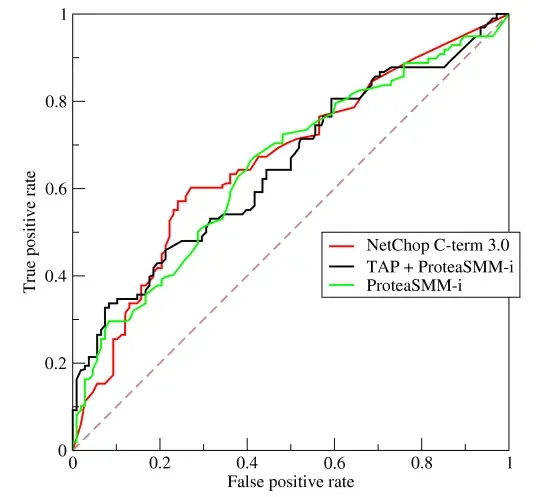
image.png

以一个简单的模拟数据来计算下ROC曲线每个点的值

• 先有一组真实分类，比如0,1,0,1,即正例为2个，反例为2个；然后一组模型预测的打分（概率），比如：0.2,0.3,0.5,0.8
• 依据上述打分依次计算每个样本输出概率下的FPR和TPR
• 首先截断点为0.2，即设定阈值为0.2，当概率大于等于0.2时，则预测为正例，因此4个样本均为正例，此时 TP = 2, FN = 0, FP = 2,TN = 0; FPR= FP / ( FP + TN ) = 2 / (2+0) = 1，TPR=TP / (TP + FN) = 2 / (2+0) = 1
• 接着截断点为0.3，即设定阈值为0.23，因此当概率大于等于0.3时预测为正例，因此样本1预测为反例，样本2-4为正例，这时的此时 TP = 2, FN = 0, FP = 1,TN = 1; FPR= FP / ( FP + TN ) = 1 / (1+1) = 0.5，TPR=TP / (TP + FN) = 2 / (2+0) = 1
• 计算截断点0.5，即设定阈值为0.5时，FPR=0.5，TPR=0.5；
• 计算截断点0.8，即设定阈值为0.8时，FPR=0，TPR=0.5；

Python可以用sklearn，R可以用ROCR包或者pROC包，这里以ROCR包来检验下上述计算结果：

library(ROCR)
y <- c(0,1,0,1)
p <- c(0.2,0.3,0.5,0.8)
pred <- prediction(p, y)
perf <- performance(pred, "tpr", "fpr")

> perf
An object of class "performance"
Slot "x.name":
[1] "False positive rate"
Slot "y.name":
[1] "True positive rate"
Slot "alpha.name":
[1] "Cutoff"
Slot "x.values":
[[1]]
[1] 0.0 0.0 0.5 0.5 1.0
Slot "y.values":
[[1]]
[1] 0.0 0.5 0.5 1.0 1.0
Slot "alpha.values":
[[1]]
[1] Inf 0.8 0.5 0.3 0.2

x.values对应FPR，y.values对应TPR, alpha.values对应预测打分cutoff，结果跟上面完全一致，然后简单做个ROC图。

library(pROC)
modelroc <- roc(y,p)
plot(modelroc, print.auc=TRUE, auc.polygon=TRUE)

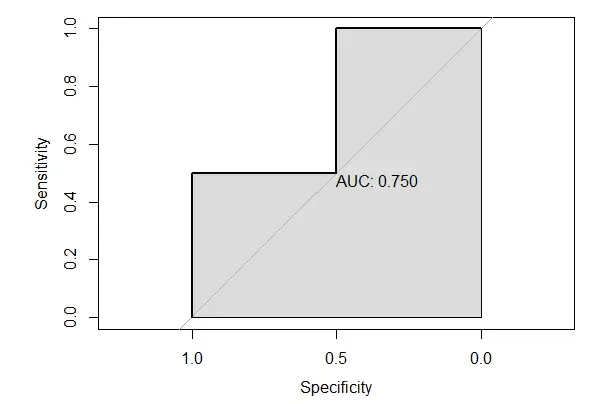
image.png

AUC

AUC的定义

AUC值就相当于ROC曲线的所覆盖的面积，可以从ROC曲线看出AUC值越大，其分类效果越好。

• AUC = 1，是完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。
• 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
• AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
• AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

如何计算AUC

• 方法一：从早期的计算ROC曲线下的面积
• 方法二：通过计算正例score大于反例score的概率：
  仍是上面的例子，真实分类：0,1,0,1，即正例为2个，记为M个，反例为2个，记为N个；模型预测的打分：0.2,0.3,0.5,0.8。
  正例有2个(0.3和0.8)，反例有2个(0.2和0.5)，那么总共有2*2=4对（[0.3,0.2],[0.8,0.2],[0.3,0.5],[0.8,0.5]）正反样本对。
  通过其模型预测的score可看出正例的score大于反例的有3对（[0.3,0.2],[0.8,0.2],[0.8,0.5]）（此处理解应为[0.3,0.2],0.3为正例，0.2为反例，0.3>0.2），因此AUC则为3/4=0.75
• 方法三：当样本比较多时，上述算法的复杂度过高O(N*M)，有人提出一个简单的算法：对score从到小排序，最大的score排序索引为n，最小的则为1；然后将正例的索引求和，减去正例-正例这种组合的个数M*(M+1)/2；最后除以M*N。
  以上述为例：(0.2,0.3,0.5,0.8) →（1，2，3，4），正例的排序索引为2和4，M和N都为2，因此AUC=(2+4-2*(2+1)/2)/(2*2)=0.75

参考链接

理解ROC和AUC
ROC曲线与AUC值

文章均来自互联网如有不妥请联系作者删除QQ:314111741 地址：http://www.mqs.net/post/14418.html