10-19：数字信号处理课程小结

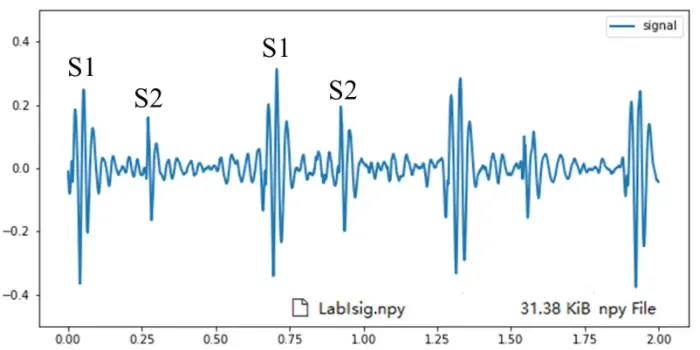
心音信号.png

老师教我们这样处理：先进行分段，然后计算每一段的局部平均能量

和每一段的局部最大值

，

指一段中的时域信号。然后我们找

的峰值，S1和S2特征会出现峰值的差异。由此我们大致区分开了S1和S2。

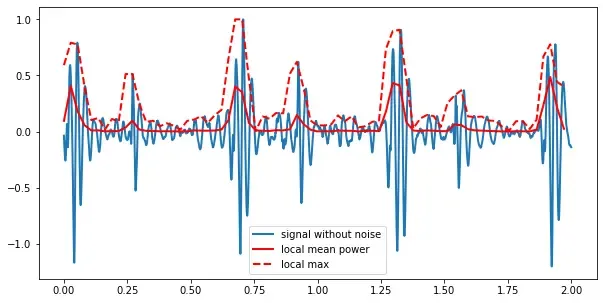
时域处理后的结果.png

3.STFT

以下代码大部分来自课上老师：

# -*- coding: utf-8 -*-
"""
Created on Sun Oct 18 16:22:25 2020

@author: qx-HW
"""
import matplotlib.pyplot as plt
import numpy as np
from numpy.lib.stride_tricks import as_strided
#时频原子参数
N = 3000
fs = 1000
alpha = 100
t = np.arange(0,N)*(1/fs)
t0 = 0.4
f0 = 0
f1 = 100
f = (f1-f0)*t+f0

sig = ((alpha/np.pi)**0.25)*np.exp(-0.5*alpha*(t-t0)*(t-t0))*np.sin(2*np.pi*f*t)
plt.figure(figsize=(12,4))
plt.plot(t,sig,linewidth=2)
plt.show()

#fft点数以及频率轴
nfft = N
half_fs = nfft//2
ff = fs*np.arange(0,half_fs+1)/(2*half_fs)

segL = 32               # 这个是每一小段的长度
overlap = 10     
def FenDuan(segL,overlap,sig,N):
    #信号分段
    #计算需要多少段 
    delta = segL-overlap
    
    # 这里算需要多少段，(N-overlap)/(M-overlap ),M表示段长
    segNum = np.int32(np.ceil((N-overlap)/delta));
    
    #扩展信号：看最后有没有多出来一点，补0处理
    padNum = segNum*delta+overlap-N
    if padNum==0:
        sigEx = sig
    elif padNum>0:
        sigEx = np.hstack((sig,np.zeros(padNum)))    
    
    #分段标签:其实就是找每一段的起始位置
    segIdx = np.arange(0,segNum)*delta
    #生成分段矩阵
    segMat = as_strided(sigEx,shape=(segNum,segL),strides=(sigEx.strides[0]*delta,sigEx.strides[0]))
    return segMat,segIdx

segMat,segIdx = FenDuan(segL,overlap,sig,N)

pMat = np.fft.fft(segMat) # (19,64)

'''
coutour([X, Y,] Z,[levels], **kwargs)
https://matplotlib.org/api/_as_gen/matplotlib.pyplot.contourf.html
是来绘制等高线的函数，X,Y确定低下的平面坐标，Z确定三维的高度坐标，levels确定轮廓线/区域的数量和位置
'''
plt.contourf(t[segIdx], ff[:pMat.shape[1]], pMat[:,0:half_fs+1].T,50)
plt.show()

plt.contourf(t[segIdx], ff[:pMat.shape[1]//2], pMat[:,:pMat.shape[1]//2].T,30)
plt.show()

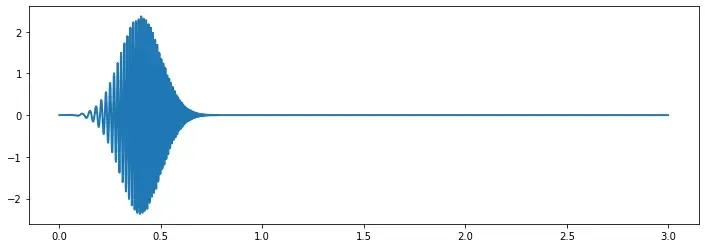
image.png

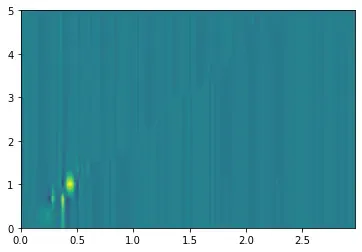
image.png

从代码上来看，就是对一个信号进行分段，然后每段做FFT，然后可视化出来。

集合网络资料和课本对短时傅里叶变换进行一些梳理和总结：

• 通过时间窗内的一段信号来表示某一时刻的信号特征。窗的长度决定频谱图的时间分辨率和频率分辨率。窗长越长，截取的信号越长。
• 信号越长，傅里叶变换后的频率分辨率越高，时间分辨率越差。相反，窗长越短，截取的信号就越短，频率分辨率越差，时间分辨率越好。
• 时间和频率是一对不可兼得的矛盾体，所以绝对意义的瞬时频率是不存在的，只能分时段。在短时傅里叶变换中，时间分辨率和频率分辨率之间不能兼得，应该根据具体需求进行取舍。

短时傅里叶变换就是先把一个函数和窗函数进行相乘，然后再进行一维的傅里叶变换。并通过窗函数的滑动得到一系列的傅里叶变换结果，将这些结果竖着排开得到一个二维的表象。

• 傅里叶变换后，横轴为频率，纵轴为幅值。短时傅里叶变换后，横轴为时间，纵轴为频率

文章均来自互联网如有不妥请联系作者删除QQ:314111741 地址：http://www.mqs.net/post/14422.html